Nature- All Mathematics
Nature, a realm vastly explored yet unconquerable! Nature and mathematics go hand in hand. Nature has helped mankind solve various mysteries yet it remains a mystery!
Take nature. As technology becomes more and more evident in the everyday lives of people, nature becomes more foreign. People need nature in their lives in order to spark their imaginations and provide experiences that are not available through any form of technology. Take mathematics. It does not deal with pencil marks, chalk marks, physical triangles or physical sets. It deals with ideas which may be represented by physical objects. It also teaches one to be precise in thoughts and words. It is difficult to find any area of life that isn’t touched by mathematics. What is more interesting is the fact that Math and nature are both tightly coupled. From rainbows, river meanders, and shadows to animal skins, spider webs and honeycombs, the visible world is full of patterns that can be described mathematically.

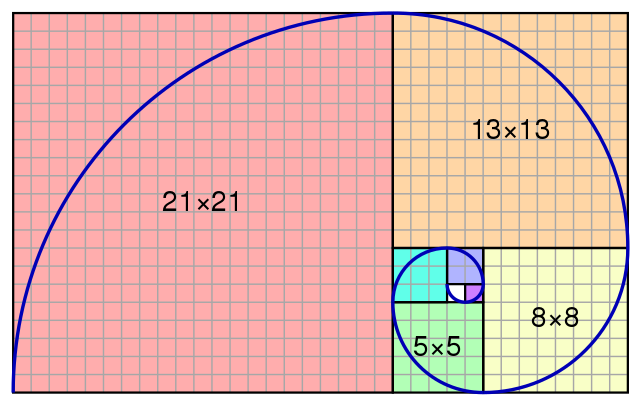
Symmetry is an integral element in mathematics which helps in resolving the complex nature of certain problems by transforming them into simpler no brainers. If you have taken enough time absorbing the essence of nature’s beauty, you ought to realize the striking symmetry that is prevalent. A day is marked with the rise of the sun and with the memory of the sun comes the picture of a Sunflower. Its beautiful pattern has its roots from the very famous Fibonacci series, whose first two numbers are both 1 and each subsequent number is the sum of the previous two. Taking our thoughts one step ahead, if we construct a series of squares with lengths equal to the Fibonacci numbers (1, 1, 2, 3, 5…..) and trace a line through the diagonals of each square, it forms a Fibonacci spiral which brings the chambers of a nautilus shell in front of our eyes!

Every one of us would have undergone that enthralling moment when our high school Math teacher introduced the very first Mathematical constant pi, besides the then known alphanumeric symbols. Any circle, even the disc of the Sun as viewed from Cappadoccia, Central Turkey, during the 2006 total eclipse, holds that perfect relationship in which, the circumference divided by the diameter equals pi. First devised (inaccurately) by the Egyptians and Babylonians, the infinite decimal places of pi (approximately 3.1415926) have been calculated to billions of decimal places.
Geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. Bacteria such as Shewanella oneidensis multiply by doubling their population in size after as short as 40 minutes. A geometric sequence such as this, where the common ratio is 2, produces a rapid increase in their population in a very short time.
Fractal is a natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. DNA, frost on the branches of a tree, lightning bolts and snowflakes are a few instances that portray the relationship where similarity holds at smaller and smaller scales. Fractals, such as the famous Mandelbrot set, cannot be represented by classical geometry.
Two interesting optimization techniques that have taken birth from what is seen in the nature are Ant Colony Optimization (ACO) and Artificial Bee Colony Algorithm (ABC).
ACO is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. In the natural world, ants (initially) lay down pheromone trails while wandering randomly, and upon finding food return to their colony. If other ants find such a path, they follow the trail. Over time, however, the pheromone trail starts to evaporate, thus reducing its attractive strength. The more time it takes for an ant to travel down the path and back again, the more time the pheromones have to evaporate. The pheromone density becomes higher on shorter paths than longer ones. Pheromone evaporation also has the advantage of avoiding the convergence to a locally optimal solution. Thus, when one ant finds a good (i.e., short) path from the colony to a food source, other ants are more likely to follow that path, and positive feedback eventually leads to all the ants’ following a single path. It has provided a breakthrough in urban transportation systems and many other fields which involve computation of shortest means to achieve the target.
ABC is an optimization algorithm based on the intelligent foraging behavior of honey bee swarm, proposed by Karaboga in 2005. Generally, bees select a small fraction of the colony to constantly forage for food sources (they are called scout bees). These scout bees on finding a highly profitable food source go to an area in the hive called the “dance floor” and perform a ritual called “the waggle dance”. The length of the dance is proportional to the scout’s rating of the food source. On seeing this dance, the other bees join the scout bee in exploitation of the flower patch. This process enables the bees to quickly switch the focus of the foraging effort on the most profitable flower patches. ABC algorithm follows a similar technique, firstly all solutions are looked upon, then solutions which are not beneficial anymore are abandoned and new solutions are now fed to enable the exploration of new regions in the search space. The applications of ABC are in the area of numerical optimization, clustering, neural network training and image processing problems.
Nature provides us with solutions to many such convoluted problems. From the flight pattern of birds used in aeronautical studies to frog’s croak pattern, many of nature’s marvels can be traced to mathematics. One concept leads to another which, yet again, leads to another! In net, nature and mathematics are realms that each tend to infinity; both are kings of their own kingdom.




